Преобразование на Лаплас
Преобразовàние на Лаплàс ℒ в математиката е интегрално преобразование, което свързва функцията на комплексна променлива (изображение, образ) с функцията на реална променлива (оригинал). То е широкоизползван метод за анализ на линейни системи, чиито характеристики не се променят с времето (на английски: Linear Time-Invariant Systems, LTI). С негова помощ се изучават свойствата на динамичните системи и се решават диференциални и интегрални уравнения.
Методът е открит от швейцарския математик Леонард Ойлер. Наречен е на името на френския математик Пиер Симон дьо Лаплас, който го използва в своята работа върху теорията на вероятностите. Наричан е също и трансформация на Лаплас.


Преобразованието на Лаплас (ПЛ) намира приложение във физиката, оптиката, електрониката, автоматиката, математическия анализ, теорията на вероятностите и обработката на сигнали.
Определение
[редактиране | редактиране на кода]Право преобразование на Лаплас
[редактиране | редактиране на кода]Правото преобразование на Лаплас на функцията на реалната променлива е функцията на комплексната променлива която е равна на интеграла на Лаплас:[1]
Обикновено оригиналът е функция, зависеща от времето, а изображението е функция на комплексната честота . Комплексната променлива (честота) се означава също чрез а функцията на изображението, получена чрез преобразование на Лаплас – с [1] Долната граница на интеграла означава , идеята на което е да се включи в интегралното преобразование делта-функцията на Дирак (наричана още „импулс“).
В литературата връзката между оригинала и изображението често се обозначава по следния начин: и и изображението обикновено се пише с главна буква.
Свойствата на тази трансформация да преобразува диференцирането и интегрирането съответно в умножение и деление, позволяват да се преобразуват интегро-диференциални уравнения в полиномни, които са много по-лесни за решаване.
Двустранно преобразование на Лаплас
[редактиране | редактиране на кода]Двустранното преобразование на Лаплас е обобщение на правото ПЛ, включващо отрицателните стойности на аргумента на функцията :
Двустранното ПЛ може да се означава и с , вместо с F.
Обратно преобразование на Лаплас
[редактиране | редактиране на кода]Обратното преобразуване на Лаплас се дава от следния комплексен интеграл, който е известен с имената интеграл на Бромвич, интеграл на Фурие–Мелин и обратна формула на Мелин:
където е реално число, е най-голямата реална част от сингулярност на така че контурната пътека на интегриране е в областта на сходимост на . В повечето приложения контурът може да бъде затворен, което позволява използването на теоремата за остатъците. В практиката тази формула се използва по-рядко. Алтернативна формула за обратното преобразуване на Лаплас е дадена от формулата за инверсия на Пост. В инженерните науки и, много често, в математиката се прибягва до таблици с функции и техните преобразования, както и до широко използване на свойствата на преобразованието на Лаплас и прилагане на обратното ПЛ за проверка. Обратното ПЛ дава функцията при ; ако , .
Пример
[редактиране | редактиране на кода]Известните обратни ПЛ са обобщени в таблици за съответствие в литературата. На практика спектралната функция обикновено трябва да се проследи обратно до тези таблични случаи, например чрез частично разлагане на прости дроби. Като пример се разглежда обратно ПЛ на спектралната функция
Може да се използва изчислението на правото ПЛ:
Обратното ПЛ е
- .
В случай на комплексни спрегнати полета, опростявания на са възможни чрез прилагане на тригонометрични тъждества.

Дискретно преобразование на Лаплас
[редактиране | редактиране на кода]Използва се в областта на компютърните системи за управление. Дискретното преобразуване на Лаплас може да се приложи към решетъчни функции.
Има -преобразование и -преобразование.
- -преобразование
Нека е решетъчна функция, т.е. стойностите на тази функция се определят само в дискретни времена , където е цяло число, а е периодът на вземане на проби. Тогава, прилагайки преобразованието на Лаплас, се получава:
- -преобразование
Ако се приложи смяната на променливите
получава се -преобразование:

Теория на вероятностите
[редактиране | редактиране на кода]В чистата и приложена вероятност преобразованието на Лаплас се определя като очаквана стойност. Ако X е случайна променлива с функция на плътност на вероятността f, тогава ПЛ на f се дава от очакването
където е очакването на случайната променлива .
По конвенция това се нарича преобразование на Лаплас на самата случайна променлива X. Тук заместването на s с −t дава функцията за генериране на моменти на X. Преобразованието на Лаплас има приложения в цялата теория на вероятностите, включително времена на първо преминаване на стохастични процеси като Марковски вериги и теория на подновяването.
От особена полза е възможността за възстановяване на кумулативната функция на разпределение на непрекъсната случайна променлива X посредством ПЛ, както следва:[2]
Алгебрична конструкция
[редактиране | редактиране на кода]Преобразованието на Лаплас може алтернативно да се дефинира по чисто алгебричен начин чрез прилагане на конструкция на поле от частни към конволюционния пръстен от функции на положителната полулиния. Полученото пространство от абстрактни оператори е точно еквивалентно на пространството на Лаплас, но в тази конструкция правото и обратно преобразования никога не трябва да бъдат изрично дефинирани (избягвайки свързаните с това трудности с доказването на конвергенция).[3]
Свойства и теореми
[редактиране | редактиране на кода]- Абсолютна сходимост
Ако интегралът на Лаплас се сближава абсолютно при , тоест има граница
тогава той се сближава абсолютно и равномерно за и е аналитична функция за ( е реалната част на комплексната променлива ). Точната долна граница на множеството от числа , за които това условие е изпълнено, се нарича абсциса на абсолютната сходимост на преобразованието на Лаплас за функцията .
- Условия за съществуване на правото преобразование на Лаплас
Преобразованието на Лаплас съществува в смисъл на абсолютна сходимост в следните случаи:
- : ПЛ съществува, ако съществува интегралът ;
- : ПЛ съществува, ако интегралът съществува за всяко крайно число и за ;
- или (която от двете граници е по-голяма): Преобразованието на Лаплас съществува, ако съществува ПЛ за функцията (производна на ) за .
Забележка: Това са достатъчни условия за съществуване.
- Условия за съществуване на обратното преобразование на Лаплас
За съществуването на обратното ПЛ е достатъчно да бъдат изпълнени следните условия:
- Ако изображението е аналитична функция за и има ред по-малък от −1, тогава неговото обратно преобразование съществува и е непрекъснато за всички стойности на аргумента и за .
- Нека , така че е аналитична функция по отношение на всяко и е равно на нула за и , тогава обратното преобразование съществува и съответното право преобразование има абсциса на абсолютна сходимост.
Забележка: Това са достатъчни условия за съществуване.
- Теорема за конволюцията
Преобразованието на Лаплас на конволюцията на два оригинала е произведение на изображенията на тези оригинали:
Доказателство на теоремата за конволюцията
|
|---|
|
Преобразование на Лаплас: За новата променлива |
- Умножение на изображения
Лявата страна на този израз се нарича интеграл на Дюамел, който играе важна роля в теорията на динамичните системи.
- Диференциране и интегриране на оригинала
Образът на Лаплас на първата производна на оригинала по отношение на аргумента е произведението на изображението и аргумента на последния минус оригинала при нула вдясно:
В по-общ случай (производна от ти ред):
Образът на Лаплас на интеграла на оригинала по отношение на неговия аргумент е образът на оригинала, разделен на неговия аргумент:
- Диференциране и интегриране на изображение
Обратното преобразуване на Лаплас на производната на изображение по отношение на неговия аргумент е произведението на оригинала и неговия аргумент, взети с противоположния знак:
Обратното преобразуване на Лаплас на интеграла на изображение върху аргумент е оригиналът на това изображение, разделен на неговия аргумент:
- Изоставане на оригинали и изображения

Забавяне (закъснение) на изображението:
Забавяне (закъснение) на оригинала:
където е функция на Хевисайд.
- Гранични теореми
Гранични теореми се наричат теоремите за начална и крайна стойност.
- , ако всички полюси на функцията са в лявата полуравнина.
Теоремата за крайната стойност е много полезна, защото описва поведението на оригинала в безкрайност, използвайки проста връзка. Това се използва например за анализ на устойчивостта на траекторията на динамична система. Теоремата е полезна и защото дава дългосрочното поведение, без да се налага рационални дроби да се разлагат на прости дроби (или други трудни алгебрични преобразования). Ако има полюс в дясната равнина или полюси на въображаемата ос [напр. ако или ], тогава поведението на тази формула е недефинирано.
- Други свойства
Умножение с число:
Обобщена таблица на свойствата
[редактиране | редактиране на кода]| Свойства на ПЛ | Оригинал на функцията Времева област |
Образ на функцията чрез ПЛ Област |
Коментари |
|---|---|---|---|
| Линейност | Резултат от основните правила на интеграция. | ||
| Първа производна на образа | е първата производна на . | ||
| -та производна на образа | По-обща форма, -та производна на . | ||
| Първа производна на оригинала | Приема се, че функцията е диференцируема и нейната производна се доближава до 0 експоненциално. Може да се получи чрез интегриране по части. | ||
| Втора производна на | Приема се, че е два пъти диференцируема, като втората производна се доближава експоненциално към безкрайност. | ||
| -та производна на | Приема се, че е пъти диференцируема и -тата ѝ производна клони към безкрайност. | ||
| Интеграл от образа | |||
| Интеграл от оригинала | е стъпаловидната функция на Хевисайд. Операторът (u * f)(t) е конволюция на u(t) и ƒ(T). | ||
| Умножен аргумент на оригинала (времева скала) |
|||
| Изместeн аргумент на образа | Това свойство понякога е известно като „Теорема за затихване“ (или „Теорема за модулация“) с . | ||
| Изместeн аргумент на оригинала | u(t) е стъпковата функция на Хевисайд (стъпкова функция). | ||
| Произведение на оригинали (конволюция на образи) |
Интегрирането се извършва по вертикалната линия Re(σ) = c, която е изцяло разположена в радиуса на конвергенция на F.[4] | ||
| Конволюция на оригинали (произведение на образи) |
ƒ(t) и g(t) са разширени до за определяне на конволюцията. | ||
| Произведение на оригинал и синус | |||
| Произведение на оригинал и косинус | |||
| Произведение на оригинал и хиперболичен синус | |||
| Произведение на оригинал и хиперболичен косинус | |||
| Сложно спрягане | |||
| Корелационна функция | |||
| Периодична функция | ƒ(t) е периодична функция с период T така че Това е резултат от свойството за изместване във времевата област и геометричния ред. | ||
| Периодично сумиране |
|
|
Право и обратно преобразование на Лаплас на някои функции
[редактиране | редактиране на кода]По-долу е дадена таблица на преобразувания на Лаплас за някои функции.
| № | Функция | Времева област |
Честотна област |
Област на сходимост за причинни системи |
|---|---|---|---|---|
| 1 | делта-функция | |
|
|
| 1a | закъсняваща делта-функция | |||
| 2 | закъсняващи от -ти ред с честотно изместване | |||
| 2a | степенна от -ти ред, | |||
| 2a.1 | степенна от -ти ред, | |||
| 2a.2 | функция на Хевисайд | |||
| 2b | функция на Хевисайд със закъснение | |||
| 2c | „бърза стъпка“ | |||
| 2d | -ти ред с честотно изместване | |||
| 2d.1 | експоненциално затихване | |||
| 3 | експоненциално приближение | |||
| 4 | синус | |||
| 5 | косинус | |||
| 6 | хиперболичен синус | |||
| 7 | хиперболичен косинус | |||
| 8 | експоненциално затихващ синус |
|||
| 9 | експоненциално затихващ косинус |
|||
| 10 | корен -ти | |||
| 11 | натурален логаритъм | |||
| 12 | функция на Бесел от първи род я , |
|||
| 13 | модифицирана функция на Бесел от първи род ред , |
|||
| 14 | функция на Бесел от втори род нулев ред |
|||
| 15 | модифицирана функция на Бесел от втори рода нулев ред |
|||
| 16 | функция на грешките | |||
Бележки към таблицата:
| ||||
Приложения на преобразованието на Лаплас
[редактиране | редактиране на кода]Преобразуването на Лаплас се използва широко в много области на математиката (операционното изчисление), физиката и техниката:
- Решаване на системи от диференциални и интегрални уравнения – с помощта на ПЛ е лесно да се премине от сложни понятия на математическия анализ към прости алгебрични отношения. [5]
- Изчисляване на предавателни функции на динамични системи, като например аналогови филтри.
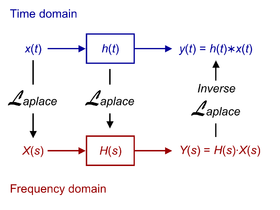
- Изчисляване на изходните сигнали на динамични системи в теорията на управлението и обработката на сигнали – тъй като изходният сигнал на линейна стационарна система е равен на конволюцията на нейната импулсна характеристика с входния сигнал, преобразованието на Лаплас позволява да се замени тази операция с просто умножение.
- Изчисляване на електрически схеми. Получава се чрез решаване на диференциални уравнения, които описват схемата с помощта на операторния метод.
- Решаване на нестационарни задачи на математическата физика.
Решаване на диференциални уравнения
[редактиране | редактиране на кода]Като цяло преобразованието на Лаплас е подходящо за решаване на линейни диференциални уравнения или системи от диференциални уравнения с постоянни коефициенти. Предимството тук е алгебраизацията: производните в областта на изображението възникват като продукт на преобразуването на Лаплас на оригиналната функция с коефициента на Лаплас . Това трансформира:
- обикновени диференциални уравнения в оригиналната област към алгебрични уравнения в областта на изображението,
- частични диференциални уравнения с независими променливи в оригиналната област до частични (или обикновени) диференциални уравнения с независими променливи в областта на изображението,
- и интегрални уравнения от тип конволюция в оригиналната област към алгебрични уравнения в областта на изображението.
Решенията на преобразуваните задачи са много по-лесни в областта на изображението, отколкото в оригиналната област. В специални случаи по този начин могат да се решават и линейни диференциални уравнения с полиномиални коефициенти.
Процедурата за решаване на диференциално уравнение с помощта на преобразованието на Лаплас е следната:
- По зададено входно въздействие се намира изображение с помощта на таблици за съответствие.
- Според диференциалното уравнение се съставя предавателната функция.
- Намира се изображението на величината на точки 1 и 2.
- Определя се оригиналът. [6]
Изчисляване на предавателни функции
[редактиране | редактиране на кода]В машиностроенето и електротехниката, особено в контролното инженерство, преобразованието на Лаплас играе основна роля, особено поради теоремата за конволюцията. Тъй като поведението на системния изход може да бъде представено в спектралния диапазон като продукт на входната функция и предавателната функция (ПФ), специфична за системата и независима от съответното възбуждане, много свойства на системата могат да бъдат определени чрез изследване на ПФ (която се получава чрез прости комбинации от елементарни предавателни функции), без да се определя изричното решение на диференциалното уравнение на системата, например чрез обратно преобразование на Лаплас. Това прави възможно, например, елегантно да се анализира стабилността на линейни непроменливи във времето системи и да се анализира поведението на вибрациите (затихване) и скоростта както на управляваните системи, така и на затворените контролни контури. Тъй като предавателната функция в диапазона на Лаплас за се променя в ПФ в диапазона на Фурие, предавателните свойства могат да се представят графично по различни начини: чрез амплитудните и фазовите честотни характеристики и чрез логаритмичната амплитудно-фазова честотна характеристика (ЛАФЧХ, диаграма на Бо́де).
Връзка с други преобразования
[редактиране | редактиране на кода]Преобразование на Фурие
[редактиране | редактиране на кода]Преобразованието на Фурие (ПФ) е частен случай (при определени условия) на двустранното преобразование на Лаплас. Докато ПФ на функция е сложна функция на реална променлива (честота), преобразованието на Лаплас на функция е сложна функция на сложна променлива. Преобразованието на Лаплас обикновено се ограничава до преобразование на функции на t ≥ 0. Следствие от това ограничение е, че ПЛ на функция е холоморфна функция на променливата s. За разлика от ПФ, преобразованието на Лаплас на разпределение обикновено е функция с добро поведение. Техники на сложни променливи също могат да се използват за директно изследване на преобразованията на Лаплас. Като холоморфна функция ПЛ има представяне в степенен ред. Този степенен ред изразява функция като линейна суперпозиция на моменти на функцията. Тази перспектива има приложения в теорията на вероятностите.
Преобразованието на Фурие е еквивалентно на оценяване на двустранното ПЛ с въображаем аргумент s = iω или s = 2πiξ,[7] когато е изпълнено условието
Тази модификация на ПФ ( в Преобразование на Фурие – Ъглова честота) изисква коефициент 12π върху обратното ПФ. Тази връзка между преобразованията на Лаплас и Фурие често се използва за определяне на честотния спектър на сигнал или динамична система.
Горната връзка е валидна, както е посочено, тогава и само тогава, когато областта на конвергенция (OК) на съдържа въображаемата ос .
Например, функцията f(t) = cos(ω0t) има преобразование на Лаплас F(s) = s/(s2 + ω02), чиято OК е Re(s) > 0. Тъй като s = iω0 е полюс на F(s), заместването на s = iω във F(s) не дава преобразованието на Фурие на f(t)u(t), което съдържа членове, пропорционални на делта функциите на Дирак δ(ω ± ω0).
Въпреки това, равенството
е в сила и при много по-слаби условия. Например, това важи за горния пример, при условие че ограничението се разбира като слабо ограничение на мерките (слаба топология). Общите условия, свързващи границата на преобразованието на Лаплас на функция с границата на преобразованието на Фурие, приемат формата на теореми на Пейли–Винер.
Вижте също
[редактиране | редактиране на кода]Източници
[редактиране | редактиране на кода]- ↑ а б Диткин В. А., Кузнецов П. И. – Справочник по операционному исчислению: Основы теории и таблицы формул. М., Государственное издательство технико-теоретической литературы, 1951. с. 256. (на руски)
- ↑ Кумулативната функция на разпределение е интеграл от функцията на плътността на вероятността.
- ↑ Mikusiński, Jan. Operational Calculus. Elsevier, 14 July 2014. ISBN 9781483278933.
- ↑ Bracewell R. N. – The Fourier Transform and Its Applications (3rd ed.), ISBN 978-0-07-116043-8, Boston: McGraw-Hill, 2000 (на английски).
- ↑ Ващенко-Захарченко М. Е. – Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений. — Киев, 1862.
- ↑ Боковой А.В. – Архитектура системы автоматического управления группой малых беспилотных летательных аппаратов // Информационные технологии и вычислительные системы, №1 (статья). Москва, ФИЦ ИУ РАН, 20.3.2018. DOI:10.14357/20718632180109. с. 68-77. Посетен на 8.4.2024 г. (на руски)
- ↑ Takacs 1953, с. 93
Външни препратки
[редактиране | редактиране на кода]- Преобразование Лапласа и его некоторые свойства (dsplib.org)Архив на оригинала от 2018-08-12 в Wayback Machine. (на руски).
- Преобразование Лапласа, exponenta.ru (на руски).
- Eric Weisstein – Laplace Transform, MathWorld (на английски).
- Laplace-Transformation: Задачи и интерактивни задачи (на немски).
- Jörn Loviscach – Laplace-Transformation von Ableitungen (Преобразование на Лаплас на производни), видео, предоставено от Библиотеката с техническа информация (TIB), DOI: 10.5446/10275, 2011 (на немски).










































![{\displaystyle {\mathcal {L}}\{f\}(s)=\operatorname {E} \!\left[e^{-sX}\right]\!,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/262eeeb0964fe497deb8329caf28844c5954e586)
![{\displaystyle \operatorname {E} \left[r\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dba567773bc69e2a3f83bd81ef6ebcd80c4c21dc)

![{\displaystyle F_{X}(x)={\mathcal {L}}^{-1}\!\left\{{\frac {1}{s}}\operatorname {E} \left[e^{-sX}\right]\right\}\!(x)={\mathcal {L}}^{-1}\!\left\{{\frac {1}{s}}{\mathcal {L}}\{f\}(s)\right\}\!(x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e5b1d7b19716a60e168d9476f56bcfecbaba3f9)




















![{\displaystyle F(s)=\varphi [F_{1}(s),\;F_{2}(s),\;\ldots ,\;F_{n}(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f161279f4e68d040d9fca85fdaf670d6eba766a7)






























































































































![{\displaystyle {\sqrt[{n}]{t}}\cdot H(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9baf26cf3fb0080262adfa0c7d67cd3757bb05f1)


![{\displaystyle -{\frac {1}{s}}[\ln(t_{0}s)+\gamma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6be541b1955df207732dd598d515f1340c721fe)




























![{\displaystyle {\begin{aligned}{\hat {f}}(\omega )&={\mathcal {F}}\{f(t)\}\\[4pt]&={\mathcal {L}}\{f(t)\}|_{s=i\omega }=F(s)|_{s=i\omega }\\[4pt]&=\int _{-\infty }^{\infty }e^{-i\omega t}f(t)\,dt~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44fd8f6a7374f8e3ae9b00c7ca0107108784f9cd)


