Уравнение

$14{\sqrt {x}}+15=71$
Най-старото известно уравнение, публикувано през 1557 година от Робърт Рекърд, който въвежда и знака „=“ за означаване на равенство

Динамичните системи се описват с уравнения, чиито решения са функции, като изобразения на графиката странен атрактор

В математиката уравнението представлява два математически израза, свързани помежду си със знак за равенство. То може да съдържа една или повече променливи. Решаването на уравнението се състои в намирането на стойностите на променливите, за които равенството е изпълнено. Променливите се наричат също така неизвестни, а стойностите, за които равенството е изпълнено – решения на уравнението. В различните езици значението на думата може да има различни значения. За разлика от тъждеството, което винаги е изпълнено за всички стойности на променливата, уравнението е равенство, което не е задължително изпълнено за всички възможни стойности на променливата, а само за определени такива.

Съществува голямо разнообразие от уравнения, които намират приложение в различни области на математиката, като методите за тяхното решаване се различават в зависимост от вида на уравнението.

В алгебрата се разглеждат две основни групи уравнения – полиномните уравнения и системите линейните уравнения. Полиномните уравнения имат общия вид P(х) = 0, където P е полиномна функция, а системите линейни уравнения – a(x) + b = 0, където a линейно изображение, а b и неизвестното x са вектори. За решаването на алгебричните уравнения се използват алгоритмични или геометрични методи, базирани на линейната алгебра или математическия анализ.

Алгебрата изследва и диофантовите уравнения, при които коефициентите и решенията са цели числа, като при тях се използват различни методи, основани на аритметиката. Тези уравнения обикновено са трудни и най-често при тях се търси само дали съществуват решения и какъв е техният брой.

В геометрията уравненията се използват за описване на различни геометрични обекти. Тук целта не е намирането на решения, а демонстрирането и изследването на определени геометрични свойства. В тази област приложение намират две големи групи уравнения – декартови и параметрични.

Математическият анализ изследва уравнения от вида f(x) = 0, където f е функция с определени свойства, като непрекъснатост и диференцируемост. Методите за решаване на тези уравнения дават възможност за конструиране на сходящи поредици от решения, като целта е да се достигне до възможно най-точното решение.

Динамичните системи се дефинират чрез уравнения, чиито решения са редици или функции на една или повече променливи. В този контекст се разглеждат два основни въпроса – за началното състояние и за асимптотичното поведение. За всяко допустимо начално състояние, например стойността на редицата или функцията в нулата, уравнението допуска определено единствено решение. Чувствителността на решенията към малки промени в началното състояние е една от основните задачи. Асимптотичното поведение на дадено решение е формата на решението при стойности на променливата, клонящи към минус или плюс безкрайност. Ако решението не е разходящо, то може да клони към дадена стойност, да има цикличен характер или да има хаотично поведение.

Общи сведения

Неизвестни, решения, тъждествени преобразувания

Следният пример е взет от книгата „Китаб ал-джабр уал-мукабала“ на Мохамед ал-Хорезми, един от основоположниците на алгебрата

Един човек умрял и оставил поравно наследството си на четиримата си сина като направил дарение на един човек, равно на дела на един от синовете си, и на друг четвърт от разликата между една трета от наследството и първото дарение. Ако с x е означен дела от наследството, който получава всеки един син, задачата се преобразува в следното уравнение, в което стойността 1 вдясно обозначава цялото наследство: $$(1)\quad 4x+x+{\frac {1}{4}}\left({\frac {1}{3}}-x\right)=1$$

В примера формулираното уравнение означава, че равенството (1) е тъждествено на описаната задача. За да се получи отговора, трябва да се определи единствената стойност на неизвестното x, за която равенството е изпълнено – решение (или корен) на уравнението. Манипулирането на неизвестното дава възможност за решаване на някои уравнения, като представеното тук. Това става чрез преобразуване на уравнението в друго, което е тъждествено на първоначалното.

Две уравнения са тъждествени, ако имат едно и също дефиниционно множество и едни и същи корени. Основните тъждествени преобразувания (начини за получаване на тъждествено на дадено уравнение) са:

• Размяна на двете страни на равенството
• Добавяне към двете страни на равенството на един и същ аритметичен израз, който не стеснява дефиниционното множество
• Умножаване на двете страни на равенството с един и същ аритметичен израз, който е различен от 0 и не стеснява дефиниционното множество (например, умножението с 1/x на уравнение от вида 5x = 0 не е тъждествено преобразование, защото изключва 0 от дефиниционното множество на променливата x)
• Степенуване на двете страни на равенството с една и съща степен, която не стеснява дефиниционното множество

Решаването на уравнението в примера може да стане по следния начин: Опростяване на израза вляво $${\frac {19}{4}}x+{\frac {1}{12}}=1$$ Добавяне на -1/12 към двете страни на равенството $${\frac {19}{4}}x={\frac {11}{12}}$$ Умножаване с 4/19 на двете страни на равенството $$x={\frac {11}{57}}$$

Параметри

Параметри в уравненията са променливи, които за разлика от неизвестните могат да присъстват и в решението. Такива уравнения се наричат параметрични и са използвани за пръв път през 16 век от Франсоа Виет като средство за общо решаване на цели групи уравнения, като тези в следния пример:

Пример за параметрично уравнение

Графиката на функцията f е парабола, показана в синьо на схемата, графиката на g1(x) е правата в червено, тази на g-2(x) – във виолетово и тази на g-1 – в зелено Търси се броят на реалните корени на следните уравнения: $$(1)\;x^{2}=2x+1,\;(2)\;x^{2}=2x-2\;{\text{и}}\;(3)\;x^{2}=2x-1$$ Задачата може да се реши, като се въведе функцията f(x), която съпоставя на всяко x стойността x2. Нейната графика е квадратна парабола, показана в синьо на схемата вдясно. Функцията g1(x) съпоставя на x стойността 2.x +1 (червената права). Корените на уравнение (1) са абсцисите на пресечните точки на параболата и червената права, като графичното представяне показва, че съществуват две решения, съответстващи на двете пресечни точки. За решаването на уравнение (2) се въвежда функцията g-2(x), която съпоставя на x стойността 2.x -2 (виолетовата права). Тя не пресича параболата, което означава, че уравнението няма решение. В последния случай се въвежда функцията g-1(x), която съпоставя на x стойността 2.x -1 (зелената права). Нейната графика е права, успоредна на първите две, която има една обща точка с параболата и съответно третото уравнение има едно решение. Задачата може да се реши по по-общ начин, като в уравненията се въведе параметър a, който може да заема произволни стойности, а трите уравнения се разглеждат като частни случаи при стойности на параметъра a 1, -2 и -1: $$(4)\quad x^{2}=2x+a$$ <

Уравнение (4) се нарича параметрично уравнение, а променливата a – параметър.

Алгебра

Полиномни уравнения

Графиката на полинома X⁵ – 3X + 2 показва, че той има поне четири корена (петият не се вижда на тази графика), и илюстрира основната теорема на алгебрата в този частен случай

Основна категория уравнения, изследвани от алгебрата, са полиномните уравнения, които имат общия вид:

$$P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{2}x^{2}+a_{1}x+a_{0}=0\!$$

където a_n ≠ 0, а стойността n се нарича степен на уравнението.

Наличието на добре разработени методи за решаването на полиномни уравнения дава възможност за решаването чрез подходяща замяна на неизвестното и на други групи уравнения. Например, уравнението e^2x – (e^a + e^b)e^x + e^a+b = 0 може да бъде трансформирано в полиномно уравнение от втора степен чрез полагането X = e^x.

Решаването на полиномните уравнения от първите няколко степени е сравнително просто. При уравненията от първа степен (линейни уравнения) решението е:

$$x={\frac {-a_{0}}{a_{1}}}\!$$

При уравненията от втора степен (квадратни уравнения) корените също може да се получат в явен вид, когато коефициентите и корените са реални числа:

$$x={\frac {-a_{1}\pm {\sqrt {{a_{1}}^{2}-4{a_{2}}{a_{0}}}}}{2{a_{2}}}}$$

където условието за реалност на корените е стойността под квадратния корен, наричана дискриминанта, да бъде по-голяма или равна на нула.

Решаването на полиномните уравнения от трета степен (кубични уравнения) е по-сложна задача. Италианските математици през Ренесанса установяват, че получаването на общо решение изисква добавянето към множеството на числата на имагинерните числа. Това откритие дава възможност за формулирането на затворени решения на уравненията от трета и четвърта степен – съответно формула на Кардано и формула на Ферари.

По-късно е изведена и основната теорема на алгебрата, според която всяко полиномно уравнение от степен по-голяма от нула и с реални или комплексни коефициенти има поне един комплексен корен. Макар че тази теорема гарантира съществуването на решение за много широк кръг полиномни уравнения, тя не предлага явно решение, а наличието на комплексни корени на уравненията с реални коефициенти не е интуитивно очевидно. Теоремата на Абел-Руфини дава обяснение на този факт, като показва, че за полиномните уравнения от по-висока степен не съществува обща формула, подобна на тези за уравненията до четвърта степен. Този извод, до който достига Нилс Абел, е допълнен от Еварист Галоа, който извежда необходимото и достатъчно условие за наличие на решение от подобен вид на полиномните уравнения. В историята на математиката основната теорема на алгебрата и теоремата на Абел-Руфини образуват популярната през 19 век теория на уравненията, която днес не се разглежда като самостоятелна област на математиката.

Системи линейни уравнения

„Дзиуджан Суаншу“, китайска книга от 2 век пр.н.е., описваща вариант на метода на Гаус за решаване на системи линейни уравнения

Друга група уравнения, изследвани от алгебрата, са векторните линейни уравнения от вида:

$$a(x)+b=0\!$$

където a е линейно изображение на векторното пространство E във векторното пространство F, b е вектор от пространството F, а x е променлива, дефинирана в пространството E.

Ако пространствата E и F са с крайна размерност, съответно n и m, изборът на база на E и F дава възможност изображението a да се представи под формата на матрица (a_jk), x – под формата на вектор стълб с n координати (x_k) и b – като вектор стълб с m координати (b_j). Така векторното линейно уравнение може да бъде записано като система от линейни уравнения:

$$\quad \left\{{\begin{matrix}a_{11}x_{1}+a_{12}x_{2}+...+a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+...+a_{2n}x_{n}=b_{2}\\\vdots \\a_{m1}x_{1}+a_{m2}x_{2}+...+a_{mn}x_{n}=b_{m}\end{matrix}}\right.$$

Системите линейни уравнения намират широко приложение в науката и техниката, често в методи за приблизително решаване на диференциални уравнения, поради което съществуват множество методи за тяхното решаване. В случая, когато размерностите n и m са равни и детерминантата на матрицата a е различна от нула, решението на системата може да бъде получено в явен вид чрез метода на Крамер. Този начин за решаване на системите е неефективен и в практиката по-често се използват итерационни алгоритми, като метода на Гаус. Неговата цел е да отдели отделните неизвестни, като чрез поредица тъждествени преобразувания получи линейни уравнения с едно неизвестно. Методът на Гаус е известен още през Древността. Негов вариант е описан в Глава 8 на китайската математическа книга от 2 век пр.н.е. „Дзиуджан Суаншу“.

Геометрична интерпретация на линейните уравнения

Геометрията дава възможност за създаване на по-ефективни алгоритми за решаване на линейни уравнения. Схемата показва триизмерно изображение на функцията f.

Схема на хоризонталите на функцията f. Червената и зелената отсечка показват пътя на приблизително решение, което се извършва с две итерации в двуизмерния случай.

Геометричната интерпретация на системите линейни уравнения дава допълнителна информация за техния характер. Изображението на линейния оператор a образува векторно подпространство, подобно на равнината в триизмерното пространство. Ядрото на a (векторите от дефиниционното множество, чието изображение е нулевият вектор) също е подпространство. Тези резултати показват, че множестовото от решенията образува афинно пространство.

Този подход дава възможност за създаване на алгоритми за решение, които отчитат характерните особености на a. В някои частни случаи съществуват методи, позволяващи по-бързото намиране на решение, отколкото чрез метода на Гаус. Например, възможно е да не се търси пряко решение на уравнението a.x + b = 0, а да се отговори на друг въпрос, привидно по-сложен – да се намери екстремума на f(x), дефинирана като:

$$\forall x\in E\quad f(x)={\frac {1}{2}}\langle ax,x\rangle +\langle b,x\rangle$$

Този екстремум е и решението на системата линейни уравнения. За да се разбере методът на решение, най-просто е да се разгледа случаят с две измерения – графиката на f има овална форма, както е показано на схемата вляво. Ако се тръгне от произволна точка x₀ и се следва кривата с най-голям наклон (показана като червена парабола на схемата вляво и като червена отсечка на схемата вдясно), най-високата точка се означава като x₁. От точка x₁ отново се следва кривата с най-голям наклон, показана в зелено на схемите. Този алгоритъм се нарича метод на най-бързото изкачване. Ако вместо да се следва точно пътя на най-големия наклон, се избере посока, ортогонална на предходните посоки, методът дава решение за максимум n стъпки, където n е броят на измеренията на E.

Геометрия

Аналитична геометрия

Коничните сечения са криви, представляващи сечение на кръгов конус и равнина

В евклидовата геометрия е възможно всяка точка от пространството да се съпоставят определени координати, например чрез използването на ортонормален базис. Този подход дава възможност геометричните фигури да бъдат описвани с помощта на уравнения. Така например, равнина в триизмерното пространство може да се опише като съвкупността от решенията на уравнение от вида a.x + b.y + c.z + d = 0, където a, b, c и d са реални числа, а неизвестните x, y и z са координатите на точките от равнината в избраната координатна система. Числата a, b и c са координати на вектор, перпендикулярен на описваната от уравнението равнина. Правата се дефинира като сечение на две равнини и може да се опише като съвкупността от решенията на линейно уравнение със стойности в ℝ² или на система от две линейни уравнения със стойности в ℝ, където ℝ е множеството на реалните числа.

Коничните сечения представляват сечения на конус с уравнение x² + y² = z² и равнина – в пространството всяко конично сечение се дефинира като множеството от точки, чиито координати са решения на уравнение на равнина и на посоченото уравнение. Тази форма дава възможност да се определи положението и свойствата на фокусите на коничните сечения.

Декартовото уравнение на окръжността дава възможност за проста демонстрация на теоремата на Талес

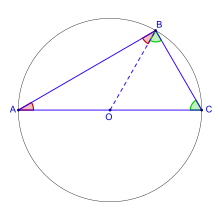
С използването на този подход могат да се получат и уравнения, чиято цел не е изразяването на решения, подобни на току-що описаните. Пример за това е теоремата на Талес, според която един триъгълник е правоъгълен, ако една от страните му е диаметър на описаната около него окръжност. При подходящ избор на правоъгълна координатна система уравнението на окръжността може да се опише като: x² + y² = 1, а точките A и C на схемата вдясно имат координати съответно (-1,0) и (1,0). Ако AB е перпендикулярна на CB, съответните вектори също трябва да са ортогонални. Така с помощта на уравнението на окръжността е лесно да се покаже верността на теоремата:

$${\overrightarrow {AB}}\cdot {\overrightarrow {CB}}=\langle (x-1,y),(x+1,y)\rangle =(x+1)(x-1)+y^{2}=x^{2}+y^{2}-1=0\quad {\text{тъй като}}\quad x^{2}+y^{2}=1$$

Използването на уравнения дава нови възможности за разрешаване на геометрични задачи. С превръщането на геометричните фигури в уравнения декартовата координатна система преобразува геометричната задача в аналитична, откъдето идва и наименованието на цялата математическа дисциплина – аналитична геометрия. Този подход, демонстриран от Рене Декарт, обогатява и напълно преобразява известната от Античността геометрия.

В наши дни аналитичната геометрия е активно развиващ се клон на математиката. В нейната основа продължава да бъде използването на уравнения за описване на геометрични обекти, но тя прилага и по-сложни методи, базирани на функционалния анализ и линейната алгебра.

Декартови и параметрични уравнения

Представянето на геометрични фигури като уравнения обикновено става по един от два основни метода. При първия се използва уравнение от вида f(x) = 0, където f е функция от евклидовото пространство E с размерност n в ℝ^d, а d е естествено число, по-малко от n. Ако f е достатъчно правилна функция, n – d е размерността на геометричната фигура – ако тя е 1, фигурата е крива, при 2 тя е повърхнина и т.н. Такова уравнение може да се представи и като система от d уравнения с реални корени. Този вид уравнения се наричат декартови, ако x е представено чрез координати в декартова координатна система. Всички уравнения в предходния раздел са декартови.

Другият често използван метод се състои в описването на геометричните фигури с помощта на функция f от ℝ^d в E по такъв начин, че една точка m в E е елемент на фигурата, когато съществува точка x в дефиниционното множество на функцията f, за която f(x) е равно на m. В този случай и при достатъчна правилност на f описаната фигура има размерност d, а уравнението се нарича параметрично. Например, единичната окръжност може да се опише с параметъра θ и параметричните уравнения:

$$\left\{{\begin{matrix}x&=&\cos \theta \\y&=&\sin \theta \end{matrix}}\right.$$

Ако описваната фигура е достатъчно правилна, например, ако поне локално съответства на дадено многообразие, то е възможно тя да се параметризира. В този контекст локално означава, че ако m е елемент на фигурата, съществува функция f и околност V на точка от дефиниционното множество f, такава че изображението на f остава част от фигурата и такова че изображението на V от f е околност на m във фигурата.

Теория на числата

Диофантови уравнения

След многовековни усилия на математическата общност Давид Хилберт пръв успява да намери решение на диофантовото уравнение от втора степен

В исторически план първите формализирани уравнения имат аритметичен характер и датират от 3 век. Ако решението на дадено уравнение се търси не като произволно число, а като цяло число, и ако уравнението е с цели коефициенти, то се нарича диофантово. Описаните по-горе методи по принцип не са достатъчни за решаването на тази група уравнения, за сметка на това са изключително полезни методите на аритметиката. Относително прост пример е линейното диофантово уравнение с две неизвестни a.x + b.y = c.

С увеличаването на степента на диофантовото уравнение решаването му става далеч по-сложно. Дори уравнението от втора степен далеч не е просто в общия случай (вижте например Теорема на Ферма-Ойлер или Уравнение на Пел). Чрез използването на специално създадени за тази цел методи и предпоставки, като метода на безкрайното спускане и малката теорема на Ферма, става възможно да се решат някои частни случаи.

Общото решение на уравнението от втора степен изисква използването на по-сложни методи, като тези на алгебричната теория на числата. Необходими са по-детайлни представи за числовите множества и изследване на крайни полета и цели алгебрични числа с помощта на теорията на Галоа. Така докато решение на алгебричното уравнение от втора степен е намерено от Хорезми още през 8 век, аналогичното диофантово уравнение е решено едва в края на 19 век от Давид Хилберт. Анализът на диофантовите уравнения често е толкова сложен, че се ограничава до определянето на съществуването на решения и техния брой.

Диофантовите уравнения намират широко приложение в областта на информатиката. Инструменти, основани на техния анализ, дават възможност за откриване и поправяне на грешки и са в основата на алгоритмите на криптологията. В основата на много шифри стоят диофантови уравнения, които се описват просто, но чието решаване изисква практически недостижимо време за обработка. Например, уравнението n = x.y, където n е фиксирано естествено число, а x и y са неизвестните, не може да се реши практически, ако n е произведение на две достатъчно големи прости числа. Това уравнение е основата на популярния алгоритъм за шифриране RSA.

Алгебрични и трансценденти числа

Алгебрично число е число, което е решение на ненулево полиномно уравнение с една променлива и рационални коефициенти (или еквивалентно - чрез изчистване на знаменатели - с целочислени коефициенти). Числа като пи, които не са алгебрични, се казва, че са трансцендентни. Почти всички реални и комплексни числа са трансцендентни.

Алгебрична геометрия

Алгебраичната геометрия е клон на математиката, изучаващ решенията на полиномни уравнения. Съвременната алгебраична геометрия се основава на по-абстрактни техники на абстрактната алгебра, особено на комутативната алгебра, с езика и проблемите на геометрията.

Основните обекти на изследване в алгебраичната геометрия са алгебраични разновидности, които са геометрични прояви на решения на системи от полиномични уравнения. Примери за най-изследваните класове на алгебрични разновидности са: равнинни алгебрични криви, които включват линии, кръгове, параболи, елипси, хиперболи, кубични криви като елиптични криви, и криви от четвърта степен като лемнискати и овали на Касини. Точка в равнината принадлежи на алгебраична крива, ако нейните координати удовлетворяват дадено полиномно уравнение. Основните въпроси на алгебричната геометрия включват изследване на точките от особен интерес като сингуларни точки, инфлексни точки и безкрайно отдалечени точки. По-сложните въпроси включват топологията на кривата и отношенията между кривите, дадени от различни уравнения.