Сила
- Вижте пояснителната страница за други значения на Сила.
| Серия статии на тема Класическа механика |

|
| Импулс · Сила · Енергия · Работа · Мощност · Скорост · Ускорение · Инерционен момент · Момент на сила · Момент на импулса
Основни понятия
Формулировки
Раздели
Закони за запазване
|
Силата е физична величина, основно понятие във физиката, мярка за взаимодействието между телата, което предизвиква или деформация (когато тялото е с крайни размери)[1][2][3][4][5] или промяна на посоката и/или големината на скоростта, с други думи получаване на някакво ускорение. Силата е векторна величина, което показва, че се характеризира както с големина, така и с посока.
Понятието за сила е известно още от дълбока древност, но философите на античността, като Аристотел и Архимед, правят фундаментални грешки при обяснението ѝ, което отчасти се дължи на комплексността на силата на триене и оттам на неадекватната представа за същността на движението в природата и неговите закони.[6] Най-основната грешка е твърдението, че за поддържане на движението е необходимо съществуването на сила, дори при постоянна скорост. Всички тези грешки са поправени от Исак Нютон, който създава трите закона за движение, които остават непроменени в продължение на 300 години. Едва през XX век, когато Алберт Айнщайн създава теорията на относителността, той обобщава законите на Нютон за скорости близки до тази на светлината и обяснява силите свързани с гравитацията и инерцията.
С развитието на модерната физика и по-точно на квантовата механика и на технологиите, учените могат да ускоряват частици до скорост, близка до тази на светлината. Те създават стандартния модел, за да опишат силите, които съществуват между частици, по-малки от атома.
Историческо развитие на понятието[редактиране | редактиране на кода]
Преди Нютон[редактиране | редактиране на кода]

Още от древността понятието за сила е признато за неразделна част от правилното функциониране на всеки един от простите механизми. Основното им предимство е прилагането на по-малко сила за сметка на действието ѝ на по-голямо разстояние при една и съща извършена работа. Анализът на характеристиките на силите в крайна сметка завършва с работата на Архимед, който е особено известен с формулирането на плавателните сили и законите, свързани с течностите.
Аристотел дава философско определение и обсъжда концепцията за силата като неразделна част от Аристотеловата космология. Според него природата се състои от четири класически елемента, които съществуват в „естествени състояния“. Аристотел смята, че това е естественото състояние на обекти с маса на Земята, като например елементите вода и земя. Той прави разлика между вродената склонност на предметите да намират своето „естествено състояние“, което води до „естествени движения“, и от друга страна неестественото или насилствено движение, което изисква продължителното и постоянно прилагане на сила.[7] Тази теория е основана на всекидневния опит за това как се движат обектите, като например постоянното прилагане на сила, за да остане каруцата в движение, но е концептуално проблематична при отчитане на поведението на стрели в полет. Силите са приложени само в началото на полета, но стрелите се движат и след това във въздуха, без забележима сила да действа върху тях. Аристотел е бил наясно с този проблем и предлага въздуха като необходимо условие и необходимата сила за продължаване на полета. Това обяснение води до още по-големи усложнения, тъй като води до извода, че във вакуум стрелите изобщо няма да се движат и отделно въздухът, и по-точно съпротивлението на въздуха, всъщност спира, а не ускорява стрелите.[8] Критиките на учението на Аристотел започват още в Ранното средновековие, слабостите му не са коригирани до XVII век. Тогава Галилео Галилей, който е повлиян от идеята на Късното средновековие, че обектите в принудително движение носят вродена сила, наречена тласък. Той извършва експерименти с търкаляне на предмети по наклонени плоскости, за да опровергае Аристотел и неговата теория за гравитацията, и показва, че предметите се ускоряват под действието на силата на тежестта до степен, която не зависи от тяхната маса, и че запазват скоростта си, освен ако на тях не действа сила, например триене.[9]
Законите за движение на Нютон[редактиране | редактиране на кода]
Първи закон[редактиране | редактиране на кода]

Първият закон на Нютон за движението гласи, че обектите продължават да се движат с постоянна скорост, освен ако върху тях не действа външна сила – резултатната сила не е нула.[10] Този закон е естественото продължение на схващането на Галилео, че постоянната скорост е свързана с липсата на резултатна сила. Нютон изказва предположението, че всеки обект с маса има вродена инерция, която функционира като основно и естествено равновесно състояние за разлика от идеята на Аристотел за „естественото състояние на покой“. Това означава, че първият закон противоречи на Аристотеловото интуитивно убеждение, че някаква сила е необходима и е длъжна да поддържа обекта в състояние на постоянна скорост. Правейки покоя физически неразличим от ненулевата постоянна скорост, първият закон на Нютон свързва пряко инерцията с концепцията за относителността и Галилеевите относителни скорости. По-специално в системи, при които обектите се движат с различна скорост, е невъзможно да се определи кой обект е в движение и кой обект е в състояние на покой. С други думи законите на физиката са едни и същи във всички инерциални отправни системи, т.е. във всички такива, свързани с Галилеевите трансформации.
Например по време на пътуване в движещ се автомобил с постоянна скорост, законите на физиката не се променят и са същите както в състояние на покой. Едно лице може да хвърли топката право нагоре във въздуха и да я хване, тъй като пада без прилагане на сила в посоката, в която превозното средство се движи. Това е вярно, въпреки че друго лице, което наблюдава движещите се превозни средства да минават край него, отбелязва, че топката следва параболичен път в посоката на движение на превозното средство. Това е инерцията на топката, свързана с постоянната скорост по посока на движение на превозното средство, топката продължава да се движи напред, макар че е хвърлена нагоре и пада надолу. От гледна точка на лицето в автомобила, превозното средство и всичко в него е в покой: светът извън колата се движи с постоянна скорост в обратната посока. Тъй като не съществува експеримент, който може да различи дали автомобилът е в покой, или външният свят, двете ситуации се считат за физически неразличими. Инерцията е приложима еднакво добре както при постоянна скорост на движение, така и при покой.
Концепцията за инерцията може да бъде допълнително обобщена в много различни форми на постоянно движение, дори и тези, които не са строго постоянна скорост. Така например моментът на инерцията или ротационната инерция на планетата Земя е това, което определя постоянството на продължителността на деня и годината. Алберт Айнщайн разширява принципа на инерцията допълнително, когато обяснява, че отправните системи с постоянно ускорение, като например тези на свободно падане, са физически равностойни на инерционни отправни системи. Този принцип на равностойност е един от фундаменталните принципи на общата теория на относителността.[11]
Втори закон на Нютон (Втори закон на механиката)[редактиране | редактиране на кода]
Съгласно Втория закон на Нютон за движението от класическата механика, дадена сила ще придава ускорение, обратнопропорционално на масата на тяло, което ускорение не зависи от скоростта на движение на системата. Този закон ни позволява да предскажем ускорението на материална точка. Записва се като:
където:
- F е силата, измерена в нютони (N);
- t е времето, измерено в секунди (s);
- p е импулсът (моментно състояние, функция на времето);
- v е скоростта, измерена в метри за секунда (m/s);
- m е масата, измерена в килограми (kg);
- a е ускорението, измерено в метри за секунда на квадрат (m/s2).
Ускорението a е векторна величина, откъдето и силата F е векторна величина с посока паралелна на ускорението. Предпоследното равенство в горното уравнение важи за тяло с непроменлива във времето маса. При разглеждане на тела с променлива маса (т.е. m = m(t)), каквито са например ракетата или совалката на тъкачен стан, трябва да се използва правилото за диференциране на произведение от две функции.
Трети закон[редактиране | редактиране на кода]
Третият закон на Нютон е в резултат на прилагането на симетрия към ситуации, в който силата може да се обясни с наличието на различни обекти. За два обекта (1 и 2), третият закон на Нютон гласи, че всяка сила, приложена към обект 1, благодарение на действието на обект 2, автоматично се придружава от сила, приложена към обект 2, дължаща се на действието на обект 1:[12]
Този закон предполага, че силите винаги се появяват като двойка действие и противодействие или акция и реакция.[10] Ако обект 1 и 2 се смятат че са в същата система, резултатната сила на системата, дължаща се на взаимодействието между обекти 1 и 2 е равна на нула, тъй като:
Това означава, че в затворена система от частици, няма вътрешни сили, които да са небалансирани, с други думи двойките сили акция-реакция между два обекта в една затворена система няма да доведат до ускорение на центъра на масата на системата. Обектите се ускоряват само по отношение един на друг, но самата система продължава да има ускорение нула. Освен това, ако външна сила действа на системата, тогава центърът на масата ще изпита ускорение, пропорционално на големината на външната сила, разделена на масата на системата.[1]
Комбинирането на втория и третия закон води до доказателството за съхраняване на импулса на системата:
интегрирайки по отношение на времето:
За система, която включва обекти 1 и 2:
С помощта на подобни аргументи е възможно да се обобщи за система от произволен брой частици.
Фундаментални взаимодействия[редактиране | редактиране на кода]
Всички сили във Вселената се основават на четири фундаментални взаимодействия. Силните и слабите ядрени сили действат само при много къси разстояния и са отговорни за взаимодействието между субатомни частици, включително нуклоните. Електромагнитната сила действа между електрични заряди и гравитационната сила действа между тела с големи маси. Всички останали сили се основават на съществуването на четирите фундаментални взаимодействия. Например триенето е проява на електромагнитна сила, действаща между атомите на две повърхности и принципът на Паули за изключването, [14], който не позволява атоми да преминават един през друг. Силите в пружини, моделирани от закона на Хук, са в резултат на електромагнитна сила и принципа на Паули, които със съвместни действия връщат обекта към неговото равновесно положение. Центробежната сила е фиктивна и се поражда само от ускоряване на ротационни отправни системи.[1]
Разработването на основни теории за силите продължава по линията на обединението на коренно различни идеи. Например Исак Нютон обединява силите, отговорни за падането на предмети на повърхността на Земята със силите, отговорни за орбитите на телата в небесната механика, като създава универсалната теория на гравитацията. Майкъл Фарадей и Джеймс Кларк Максуел показват, че електрическите и магнитните сили са обединени чрез една стройна теория на електромагнетизма. През ХХ век развитието на квантовата механика довежда до съвременното разбиране, че първите три фундаментални сили (всички с изключение на гравитацията) са проявления на материята (фермиони) и нейното взаимодействие чрез обмен на виртуални частици наречени калибровъчни бозони.[15] Въпреки големия напредък в обединяването на теориите, все още има много нерешени въпроси. Физиците все още се опитват да развият самостоятелни модели, които да обединят всички сили, да съчетаят четирите фундаментални взаимодействия в така наречената теория на всичко. Най-популярният подход към отговора на този въпрос е струнната теория.
Гравитационно взаимодействие[редактиране | редактиране на кода]
То е най-слабото от всички фундаментални взаимодействия и макар да действа между обекти с всякаква маса, обикновено става забележимо между масивни тела на огромни разстояния. Гравитационното взаимодействие се нарича още сила на тежестта. В рамките на класическата механика се описва със закона за всеобщото привличане, формулиран от Нютон в неговия труд „Математически начала на натурофилософията“. Големината на силата на привличането е право пропорционална на масите и обратно пропорционална на квадрата на разстоянието между телата.[16]
Където − универсалната гравитационна константа[17]
Теорията на Нютон добре описва движението на планетите от слънчевата система и много други небесни тела, но е неприемлива за движението на тела, които се движат със скорост, близка до скоростта на светлината или за масивни обекти като черните дупки, както и при променливи гравитационни полета.[18].
Обобщаваща теория на гравитационното взаимодействие е общата теория на относителността на Алберт Айнщайн. В нея гравитацията не се характеризира с инвариантна сила, която не зависи от избора на отправна система, а вместо това като свободно движение на телата в гравитационно поле с променлива скорост, разглеждано като движение по инерция в изкривеното четиримерно пространство-време, в което времето в различните точки тече различно. Изкривяването на пространството зависи от масата на телата и видовете енергия в системата.[1]
Електромагнитно взаимодействие[редактиране | редактиране на кода]
Електромагнитната сила е силата, действаща върху заредена частица, причинена от електрическото, магнитното или електромагнитно полета на средата, в която тя се намира.
Електромагнитното взаимодействие съществува между частици, които имат електричен заряд. От гледна точка на квантовата теория на полето електромагнитното взаимодействие се пренася от безмасовите бозони – фотоните. Самият фотон няма електричен заряд, а това означава че не може да взаимодейства непосредствено с други фотони. В електромагнитните взаимодействия участват също кварки, електрон, мюони и тау-лептони (фермиони), а също така и калибровъчни W^{\pm} бозони. Електростатичното взаимодействие се дава със закона на Кулон:
Подобно на гравитационното взаимодействие, тази сила намалява с квадрата на разстоянието и е пропорционална на двата заряда. За разлика от гравитационното обаче, тази сила може да е както на привличане, така и на отблъскване, а също така е няколко порядъка по-силна. Електромагнитното взаимодействие се описва от класическата електродинамика. Електромагнитната сила (или силата на Лоренц) се дава от уравнението:
Електромагнитните сили и взаимодействия са разбрани едва след съставянето на уравненията на Максуел.[19]
Силно ядрено взаимодействие[редактиране | редактиране на кода]
Силното ядрено взаимодействие действа на много малки разстояния – от порядъка на атомното ядро. На него се дължи привличането между нуклоните в ядрата. Описва се от съвременната квантова хромодинамика, която обяснява огромен брой закономерности във физиката на силното взаимодействие посредством така наречения стандартен модел. Единственият липсващ елемент в стандартния модел е бозона на Хигс. Очаква се хипотезата за неговото съществуване да бъде потвърдена и доказано с Големия адронен ускорител в ЦЕРН. В силното взаимодействие участват кварките и глуоните, а също така съставените от тях елементарни частици, наречени адрони (най-известни примери за адрони са протоните и неутроните, изграждащи голяма част от познатата ни материя).
Слабо ядрено взаимодействие[редактиране | редактиране на кода]
Слабото ядрено взаимодействие също действа на много малки разстояния, но е значително по-слабо от електромагнитното и силното ядрено взаимодействия. Характерна черта при слабото взаимодействие е сравнително голямото време на живот на частиците и тяхната колосална проникваща способност. В слабото взаимодействие участват всички основни фермиони (лептони и кварки) и техните античастици. То е отговорно за радиоактивния разпад на субатомните частици, както и за процеса, известен като ядрен синтез в звездите. Слабото взаимодействие засяга всички известни фермиони, т.е. частици, чийто спин (собствена характеристика на всички частици) е половин цяло число. В стандартния модел на физиката на елементарните частици съществува теория, според която появата на слабото взаимодействие се причинява от замяната (емисионна или на поглъщане) на W и Z бозони, и тъй като е следствие от емисии (или поглъщане) на бозони, се явява безконтактна сила. Най-известният ефект от тази емисия е бета разпадът.
Нефундаментални сили[редактиране | редактиране на кода]
Сила на реакция на опората[редактиране | редактиране на кода]
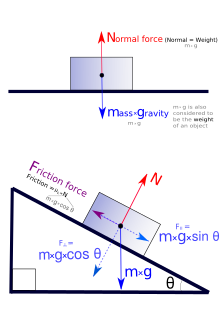
В механиката, нормалната сила (понякога отбелязвана с N) е компонентата на контактната сила, перпендикулярна на повърхността, където се осъществява този контакт и упражнявана върху обект, например на повърхността на пода или на стената.
На микрониво нормалната сила е силата на отблъскване между атомите при близък контакт.[20]
Сила на триене[редактиране | редактиране на кода]
Триенето е процес на взаимодействие на твърдите тела при относителното им движение в твърда, газообразна или течна среда. Триенето по принцип има електронна природа. Коефициентът на триене е число, характеризиращо степента на сцепление между две повърхности. Съществува статичен (в покой) и динамичен (в движение) коефициент на триене, като статичният е винаги по-голям от динамичния. Силата на триене е пропорционална на коефициента на триене и на нормалната сила (реакцията на опората):
където Ff е силата на триене, Fn е силата, перпендикулярна на контактната повърхнина, а μf е коефициентът на триене. Частен случай на сила на триене е съпротивлението на въздуха.
Сила на опъване[редактиране | редактиране на кода]
Силата на опъване във физиката се наблюдава при въжета, вериги, или кабели и е винаги успоредна на тях. Измерва се в N както всяка сила. Въжето или кабелът се считат с пренебрежима маса в сравнение с предмета, окачен на тях.
Сила на усукване[редактиране | редактиране на кода]
Силата на усукване (или известна по-скоро като момент на силата) предизвиква въртене. Математически моментът на силата се изразява с векторното произведение:
където
- е радиус-векторът или векторът на позицията на частицата (нарича се още рамо)
- е силата, действаща на частицата.
Може да се използва вторият закон на Нютон за алтернативна дефиниция на момент на силата[21].
където
- е инерционният момент на частицата
- е ъгловото ускорение на частицата
Единиците за измерване на момента на силата са N.m.
Центростремителна и центробежна сила[редактиране | редактиране на кода]

За един обект, който се движи по окръжност, небалансираната сила, действаща на обекта, наречена центростремителна, се дава с формулата:[22]
където е масата на обекта, е линейната му скорост, е разстоянието от центъра на окръжността и е единичния вектор с посока навън от центъра. Това означава, че центростремителната сила е насочена винаги към центъра на окръжността и е перпендикулярна на вектора на скоростта, което означава, че не може да промени стойността на вектора на скоростта на обекта, само неговата посока. Центростремителната сила винаги действа перпендикулярно на посоката на движение на тялото. В случая, когато обектът се движи по дъга от окръжност с променлива скорост, пълната сила се разлага на перпендикулярна компонента, която променя посоката на движение (центростремителна компонента), и паралелна или тангенциална компонента, която променя скоростта.
За разлика от центростремителната, центробежната сила е пример за фиктивна сила (наречена още псевдосила), която се появява в неинерциални отправни системи. Тя е инерционна сила и е насочена навън от центъра на въртене. Измерва се в Нютони и е пропорционална на ъгловата скорост ω. Центробежната сила се появява тогава, когато за отправна система се използва въртяща се система по отношение на инерциална отправна система. В инерциалните отправни системи центробежната сила изчезва.
Еластична сила[редактиране | редактиране на кода]

Еластичната сила е свързана с еластични материали, като пружини и ластик. Това е силата, която връща материала в равновесното му състояние, или с началната му дължина. Една идеална пружина може да бъде разтегната до безкрайност, не може да се счупи и няма маса или триене.[23]
Тази линейна зависимост е изследвана от Робърт Хук през 1676 г. и е наречена на него – закон на Хук. Ако е преместването, силата за идеална пружина е:
където константата на пружината, която е специфична за дадена пружина. Минусът означава, че е в посока, обратна на приложената сила.[1]
Консервативни и неконсервативни сили[редактиране | редактиране на кода]
Единици за сила[редактиране | редактиране на кода]
Силата се измерва с няколко различни единици:
- Нютон – това е единицата за сила в SI със символ N, тя се определя по следния начин: 1 N e силата, необходима за придаване на ускорение от 1 m/s² на тяло с маса 1 kg или силата, придаваща импулс от 1 kg.m/s. Нютонът е производна единица и се равнява на kg × m × s-2
- Дина – това е единицата за сила в CGS, чийто символ е dyn. Дефинира се по следния начин: 1 dyn e силата, която придава на маса 1 g ускорение от 1 cm/s. Връзката ѝ с нютона е 1 dyn = 1 g·cm/s² = 10−5 kg·m/s² = 10 µN
- Килограм-сила – това е стара мярка за сила, нейният символ е kgf и 1 kgf = 9,80665 N
- Планковска сила – това е една от производните единици в системата единици на Планк, която се равнява на:
- Стен
| Нютон (SI) |
Дина | Килограм-сила | Паунд-сила | Паундал | |
|---|---|---|---|---|---|
| 1 N | ≡ 1 kg·m/s² | = 105 dyn | ≈ 0.10197 kp | ≈ 0.22481 lbF | ≈ 7.2330 pdl |
| 1 dyn | = 10−5 N | ≡ 1 g·cm/s² | ≈ 1.0197×10−6 kp | ≈ 2.2481×10−6 lbF | ≈ 7.2330×10−5 pdl |
| 1 kp | = 9.80665 N | = 980665 dyn | ≡ gn·(1 kg) | ≈ 2.2046 lbF | ≈ 70.932 pdl |
| 1 lbF | ≈ 4.448222 N | ≈ 444822 dyn | ≈ 0.45359 kp | ≡ gn·(1 lb) | ≈ 32.174 pdl |
| 1 pdl | ≈ 0.138255 N | ≈ 13825 dyn | ≈ 0.014098 kp | ≈ 0.031081 lbF | ≡ 1 lb·ft/s² |
Вижте също[редактиране | редактиране на кода]
Източници[редактиране | редактиране на кода]
- ↑ а б в г д Feynman, R. P., Leighton, R. B., Sands, M. Lectures on Physics, Vol 1. Addison-Wesley, 1963. ((en))
- ↑ Kleppner, D., Kolenkow, R. J. An introduction to mechanics. McGraw-Hill, 1973. ((en))
- ↑ University Physics, Sears, Young & Zemansky, pp. 18 – 38 ((en))
- ↑ Хайкин С. Е.Силы инерции и невесомость. Изд-во „Наука“ М., 1967, с илл.((ru))
- ↑ Glossary // Earth Observatory. NASA. Архивиран от оригинала на 2008-10-12. Посетен на 9 април 2008. ((en))
- ↑ Heath, T.L. The Works of Archimedes (1897). The unabridged work in PDF form (19 MB) // Archive.org. Посетен на 14 октомври 2007.
- ↑ Land, Helen The Order of Nature in Aristotle's Physics: Place and the Elements (1998)
- ↑ Hetherington, Norriss S. Cosmology: Historical, Literary, Philosophical, Religious, and Scientific Perspectives. Garland Reference Library of the Humanities, 1993. ISBN 0815310854. с. 100.
- ↑ Drake, Stillman (1978). Galileo At Work. Chicago: University of Chicago Press. ISBN 0-226-16226-5
- ↑ а б Newton, Isaac. The Principia Mathematical Principles of Natural Philosophy. Berkeley, University of California Press, 1999. ISBN 0-520-08817-4. This is a recent translation into English by I. Bernard Cohen and Anne Whitman, with help from Julia Budenz.
- ↑ DiSalle, Robert. Space and Time: Inertial Frames // Stanford Encyclopedia of Philosophy. 30 март 2002. Посетен на 24 март 2008.
- ↑ Henderson, Tom. Lesson 4: Newton's Third Law of Motion // The Physics Classroom. 1996 – 2007. Архивиран от оригинала на 2011-08-24. Посетен на 4 януари 2008.
- ↑ Dr. Nikitin. Dynamics of translational motion // 2007. Архивиран от оригинала на 2009-09-11. Посетен на 4 януари 2008.
- ↑ Nave, R. Pauli Exclusion Principle // HyperPhysics***** Quantum Physics. Посетен на 2 януари 2008.
- ↑ Fermions & Bosons // The Particle Adventure. Архивиран от оригинала на 2007-12-18. Посетен на 4 януари 2008.
- ↑ University Physics, Sears, Young & Zemansky, pp. 59−82 ((en))
- ↑ Sir Isaac Newton: The Universal Law of Gravitation // Astronomy 161 The Solar System. Посетен на 4 януари 2008. ((en))
- ↑ Новикова, И. Д. Физический энциклопедический словарь. М.: Советская энциклопедия, 1984. с. 772−775.
- ↑ Scharf, Toralf. Polarized light in liquid crystals and polymers. John Wiley and Sons, 2007. ISBN 0471740640. с. 19., Chapter 2, p. 19
- ↑ Cutnell,. Physics, Sixth Edition. John Wiley & Sons Inc. ISBN 047123124X. с. 93.
- ↑ Newton's Second Law for Rotation // HyperPhysics Mechanics Rotation. Посетен на 4 януари 2008.
- ↑ Nave, R. Centripetal Force // HyperPhysics***** Mechanics ***** Rotation.
- ↑ Elasticity, Periodic Motion // HyperPhysics. Georgia State University. Посетен на 4 януари 2008.





























